您好!欢迎您来到工程管理硕士网!
23MEM备考 | 必看高频管综数学核心公式汇总!
发布时间:2022-11-10 10:06:56 浏览量:
对于很多MEM考生来说数学无疑是一大短板,尤其是对于那些工作时间较长的备考生们,所以大家在复习的时候一定要掌握考试答题技巧,这样才能够快速得分不耽误做题时间。
1
应用题核心公式
1. 比例问题
(1) 三个数的比的问题∶ 常用赋值法
若甲∶乙=a∶ b,乙∶丙=c∶d,
则甲∶乙∶丙= ac∶ bc∶ bd
(2) 增长率问题∶ 常用赋值法
b=a(1+x)n(设基础变量为a,平均增长率为b,增长了n期,期末值为b)
2. 行程问题∶路程=速度 * 时间
(1)相遇∶甲的速度 * 时间+乙的速度 * 时间=距离之和
(2)追及∶追及时间=追及距离 * 速度差
(3)迟到∶实际时间-迟到时间=计划时间
(4)早到∶实际时间+早到时间=计划时间
(5)相对速度问题
①迎面而来,速度相加;同向而去,速度相减
②航行问题:顺水速度=船速+水速;逆水速度=船速-水速
3. 工程问题∶工作效率=工作量/工作时间
(1)常用等量关系∶各部分的工作量之和+没干完的工作量=总工作量=1
(2)给水排水问题∶原有水量+进水量=排水量+余水量
4. 利润问题
(1)利润=销售额-成本
(2)利润率=利润÷成本×100%
5. 液问题∶浓度=溶质/溶液×100%
溶液配比问题∶将不同浓度的两种溶液,配成另外一种浓度的溶液,使用十字交叉法。
6. 集合问题
(1)A 或 B=A+B-A 且 B
(2)A 或 B 或 C=A+B+C-A 且 B-A 且 C-B 且 C+A 且 B 且 C
7. 最值应用题
(1)根据题意,化为一元二次函数求最值
(2)根据题意,化为均值不等式求最值
(3)根据题意,化为解不等式问题
2
根的判别式

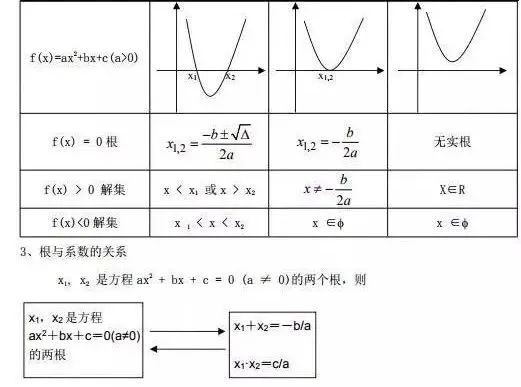

3
数列
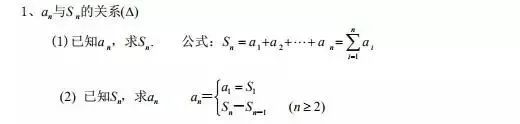




4
排列组合概率



5
实数


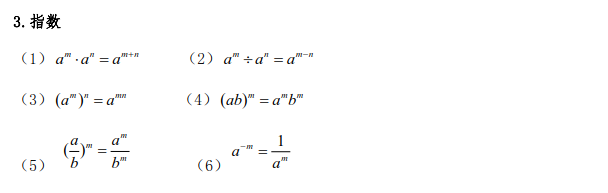
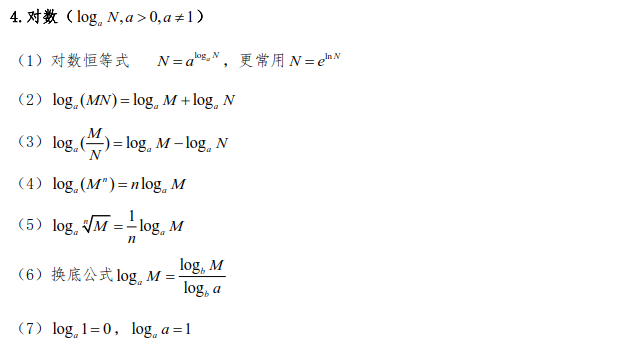

6
绝对值


7
因式分解问题
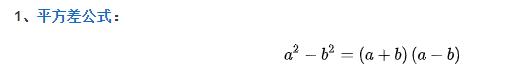
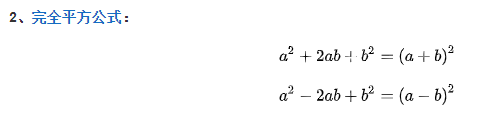

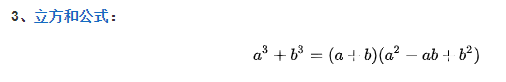
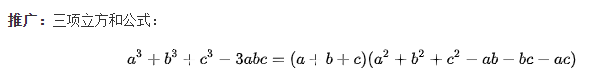
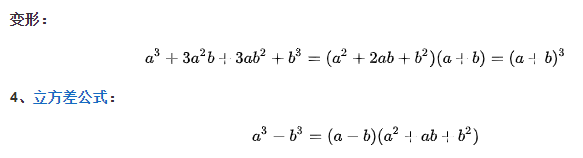
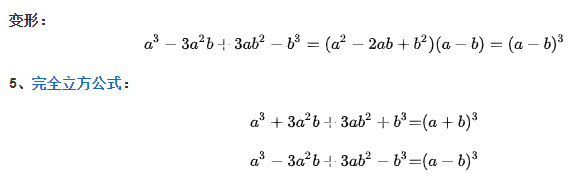
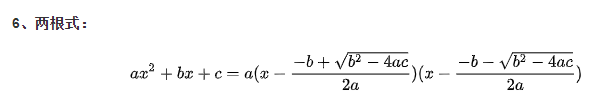
8
函数问题
一元二次函数 y=ax²+bx+c(a≠0)的最值问题,应该按以下步骤解题∶
(1)先看定义域是否为全体实数;
(2)若定义域为全体实数,则可判断y的最值。
(3)若定义域不为全体实数,则需要画图像,根据图像的最高点和最低点求解最值。
9
均值不等式问题
1. 使用均值不等式求最值
(1)口诀
一"正"二"定"三"相等";
"正"是用均值不等式的前提;
"定"是用均值不等式的目标;
"相等"是最值取到时的条件。
(2)常用拆项法,拆项必拆成相等的项,拆项常拆次数较小的项。
(3)和为定值积最大,积为定值和最小。
2. 常考用均值不等式证明不等式,但遇到此类问题仍应该先考虑特殊值法。
3. 对勾函数
函数y=x+x/1(或y=ax+b/x,a≠0,b≠0)的图像形如两个"对勾",因此将这个函数成为对勾函数,当x>0时,此函数有最小值2;当x<0时,此函数有最大值-2。
10
几何面积
1. 三角形
(1)求三角形的面积∶
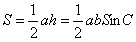
(2)三角形的相似与全等
①相似是重点,常考两种用法∶
一是求直线的长度;
二是面积比等于相似比的平方。
②遇到既有三角形,又有平行线的图形,一般都是考查相似三角形。
③全等∶折叠问题
(3)勾股定理
(4)三角形的心
内心∶ 内切围的圆心、角平分线的交点
外心∶ 外接圆的圆心、三条边的垂直平分线的交点
重心∶ 中线的交点
垂心∶ 高线的交点
2. 平行四边形面积∶ S=bh=absinφ
3. 梯形面积∶ S=中位线×高=1/2(上底+下底)×高
4. 阴影部分面积
(1)常规方法
①常用割补法,将不规则图形转化成规则图形
②要注意图形之间的等量关系
③根据对称性解题也是常见解法
(2)快速得分
真题中出现的图形,一定是准确的,所以用尺子或量角器量一下,再进行估算是简单有效的方法。
(3)其他组合图形问题
组合图形问题一般是求面积,偶尔会出现求周长、线段等问题。
11
立体几何问题




12
点与直线的位置关系



13
直线与直线的位置关系
1. 平行
(1)若两条直线的斜率相等且截距不相等,则两条直线互相平行。
(2)若两条平行直线的方程分别为
L1∶Ax+By+C1=0,L2∶Ax+By+C2=0,
那么 L1 与 L2 之间的距离为∶
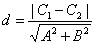
2. 相交
(1)联立两条直线的方程可以求交点∶
(2)若两条直线L1∶y=k1x+b,与 L2∶y=k2x+b,且两条直线不是互相垂直的,则两条直线的夹角a满足如下关系:
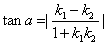
3. 重直
若两条直线互相垂直,有如下两种情况∶
(1)其中一条直线的斜率为0,另外一条直线的斜率不存在,即一条直线平行于x轴,另一条直线平行于y 轴
(2)两条直线的斜率都存在,则斜率的乘积等于一1
以上两种情况可以用下述结论代替∶
若两条直线∶
L1∶ A1x+B1y+C1=0,
L2∶ A2x+B2y+C2=0互相垂直,则A1A2+B1B2=0
14
点、直线、圆的位置关系
1. 点与圆的位置关系
点P(xo,yo),圆(x-a)2+(y-b)2 = r2,则
(1)点在圆内∶(xo-a)2+(yo-b)2 < r2
(2)点在圆上∶(xo-a)2+(yo-b)2 = r2
(3)点在圆外∶(xo-a)2+(yo-b)2 > r2
2. 直线与圆的位置关系
设圆心到直线的距离为d,圆的半径是r,则
(1)相离∶ d > r
(2)相切∶d = r
(3)相交∶ d < r
3. 圆的切线
求圆的切线方程时,常设切线的方程为Ax+By+C=0,或 y=k(x-a)+b,再利用点到直线的距离求半径,即可确定切线方程。
设圆心到直线的距离为d,圆的半径是r1,r2,则
(1)相离∶d > r1+r2
(2)相切; d = r1+r2
(3)相交∶|r1-r2| < d < r1+r2
(4)内切; d = |r1-r2|
(5)内含∶ d < |r1-r2|
易错点∶
(1)如果题干中说两个圆相切,一定要注意可能存在两种情况,即内切和外切。
(2)两圆位置关系为相交、内切、内含时,涉及两个半径之差,如果已知半径的大小,则直接用大半径减小半径,如果不知半径的大小,则必须加绝对值符号。
15
面积和对称问题
1. 常规题型
(1)求直线构成的三角形面积,求出交点坐标即可。
(2)求正方形或菱形面积,通过交点求出边长即可。
(3)求组合图形的面积,用割补法。
2. 面积的一半
如果一条直线把一个圆或者一个矩形的面积分成了一半,则这条直线必过圆的圆心或矩形的中心。
3. 其他问题
真题的解析几何问题中,一般少量出现求组合图形的周长问题。
版权声明:本文内容整理自网络,如有侵权请电话联系17800253047。转载请注明来源!
更多院校MEM项目招生信息请戳链接:http://yuanxiao.mxmem.com/
MEM工具箱

立即申请工程管理硕士(MEM)
管理类联考历年真题

全国MEM报名服务中心

第一时间获得意向MEM院校的招生政策

直接对话MEM招生办公室邀请您拜访学校、参加公开课

独家奖学金申请指导
热门院校排行榜






